Simple Quant Labs

이자율과 기회비용

쉬운것부터 시작해봅시다 😊
이자율 또는 이율은 화폐를 보유하는 경우 생기는 일종의 기회비용입니다. 화폐를 보유하지 않고 예금을 하면 이자가 생기지만, 그냥 보유한다면 그런 이자를 포기하는 셈이므로 일종의 기회비용이라 할 수 있습니다.

금리와 주가 (그리고 암호화폐)의 관계

일반적으로 금리변동과 주가의 관계는 단기적인 효과보다 중장기적인 영향을 미치곤 하며, 경기 순환과 유기적인 관계를 맺으면서 통상 반대로 움직이는 경향이 있습니다. 단기적으로 이자율이 오르면 주가에 (그리고 암호화폐도) 부정적인 영향을 주고, 이자율이 내리면 주가 (그리고 암호화폐)에 긍정적인 영향을 주는 것으로 알려져 있습니다. 그러나 항상 그런 패턴을 기계적으로 보여주는건 아닙니다. 국내에서는 이자율이 내리면 주식시장에 투자하는 대신 대출을 받아 부동산시장에 투자하는 경우도 많습니다. 그리고 완만한 경기상승이라면 장기적으로 이자율도 오르고 주가도 오를 수 있습니다. 이자율은 실물경제에 큰 영향을 미치는데 1980년대 초 미국 연방준비제도이사회가 단기금리를 급격히 올리는 바람에 미국을 더블딥 불황으로 몰아넣는 것을 보면 이자율은 매우 중요한 요소입니다. 비슷하게 2021~2022년 미국 연준(Fed)의 금리 인상 사이클은 주식 시장과 암호화폐 시장 모두에 강한 하방 압력을 가했습니다.

현금흐름과 시간가치

'현금흐름' 이라는 단어는 재무나 금융 분야에서 자주 사용하는 말이지만, 일상에서 보면 매월 납입하는 정기적금, 할부금, 또는 매월 받는 연금 등 일정한 기간 동안 여러 번의 현금이 오고 가는 것을 의미합니다. 현금흐름은 시간을 두고 일어나고, 우리는 그 현금흐름의 현재가치 또는 미래가치를 가늠해야 금융 또는 재무에 관한 현명한 의사 판단이 가능합니다. 예를 들어 성과급을 나중에 받는 것보다는 지금 받는 것이 더 가치가 있다고 많은 사람들이 판단할 수 있겠죠 (현재의 돈이 미래의 돈보다 가치가 크다). 이것처럼 돈은 시간 가치를 갖습니다. 그리고 이 시간 가치를 만드는 동력은 이자율 또는 할인율입니다. 이자율은 미래 가치를 계산하고 할인율은 현재가치를 계산합니다.

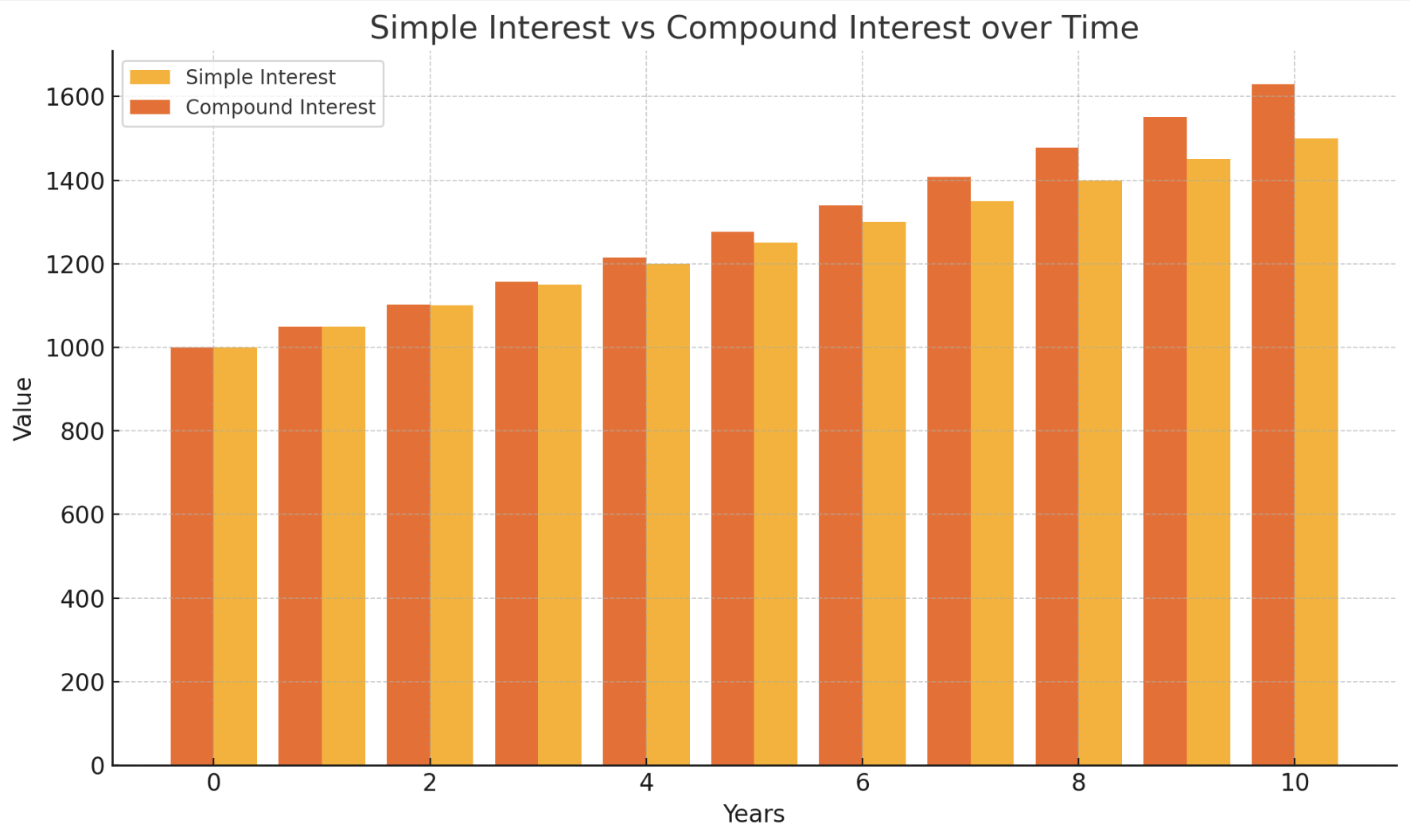
단리 (simple) vs 복리 (compound)

미래가치는 단리 또는 복리 (연속복리 포함)로 계산할 수 있습니다. 단리는 최초의 금액을 대상으로 이율을 곱해 미래가치를 계산하고, 복리는 일정 기간마다 이자를 원금에 합쳐 그 합계 금액에 대한 이자를 다시 계산합니다. 복리는 원금에 대해서만 이자를 계산하는 단리보다 이자가 당연히 더 많이 붙죠.

$$ \text{단리: 원금} \times (1 + \text{이율} \times \text{기간}) $$ $$ \text{복리: 원금} \times (1 + \text{이율})^{\text{기간}} $$

단리이자 계산

은행에 1000만원을 예금하고 1년 후에 인출하기로 했다고 하면 1년 후 받는 금액을 단리로 계산하면

$$ \text{1년 후 인출액} = 1000\text{만원} \times (1 + 5\% \times 1) = 10,500,000\text{원} $$

단위 일치의 중요성

여기서 주의할 점은 이율과 기관의 단위가 같아야 합니다. 이자율은 보통 연 단위로 표시합니다. 연간 5%의 이율은 1년간 5%의 이자를 주겠다는 뜻입니다. 그리고 기간도 1년이므로 기간이 서로 일치합니다. 만일 월 단위로 바꿔 계산한다면, 이율은 12로 나누고, 기간도 년이 아니라 월이므로 1이 아닌 12가 됩니다. 단리 계산을 월 단위로 바꿔봅시다. 인출액은 같다는걸 볼 수 있을 겁니다. $$ \text{1년 후 인출액} = 1000\text{만원} \times \left(1 + \left(\frac{5\%}{12}\right) \times 12 \right) = 10,500,000 \text{원} $$

복리이자 계산

이율과 기간의 단위가 같은게 중요한 점이 복리 계산 때문입니다. 단리는 차이가 없지만 복리는 차이가 크죠. 가령 이율 5%를 월 복리로 계산한다면, 월마다 생기는 이자에 대한 이자를 누적해 계산한다면 복리 공식에 따라 다음고 같습니다. $$ \text{1년 후 인출액} = 1000\text{만원} \times \left(1 + \frac{5\%}{12} \right)^{12} = 10,511,619 \text{원}$$

연속복리와 오일러 상수

이제 재밌는 수학 상식에 대해서 알아봅시다. 연속 복리라는게 있는데, 이건 복리 계산에서 복리 횟수를 무한정 늘려놓은 것입니다. 복리 횟수가 커지면 커질수록 복리의 효과가 커져 수익률은 늘어납니다. 따라서 일반적인 복리는 연속 볼기를 초과하지 못합니다. 연속 보리 공식은 다음과 같습니다 $$ \text{연속복리: 원금} \times e^r $$ 연속복리 공식에서 e는 오일러 상수 이고 e \approx 2.71828182845904.... 입니다. 복리 공식과 연속복리 공식은 같아요 복리 계산 공식 $$ \text{원금} \times (1 + \text{이율}) ^ \text{기간} $$에서 기간은 사실상 복리 횟수입니다. 이 횟수를 늘려가면 오일러 상수에 근접하게 된다는걸 실험적으로 알 수 있습니다. 예시 계산으로 원금 1원, 연간 이유 100% 라고 잡으면

1년 후 이율 100%, 기간 1이므로 $$ 1 \times (1 + 1)^1 = 2 $$ 분기 복리라면 이율은 100%/4, 기간 4이므로 $$ 1 \times \left(1 + \frac{1}{4} \right)^4 = 2.4414 $$ 매주 복리라면 이율은 100% / 52, 기간 52이므로 $$ 1 \times \left(1 + \frac{1}{52} \right)^{52} = 2.688373... $$ 매초 복리라면 이율은 100% / 31536000, 기간 31536000 이므로 $$ 1 \times \left(1 + \frac{1}{31536000} \right)^{31536000} = 2.71828... $$

이자율 계산은 numpy financial의 fv() 함수를 통해서 구할수도 있고 단순 파이썬 스크립트로도 쉽게 계산 가능합니다.