Simple Quant Labs

ETS (Error-Trend-Seasonality) Model

Exponential smoothing은 통계 모형이 아니고 단순하게 미래를 예측하는 방법론으로 해석할 수 있습니다. 통계 모형은 예측치에 대한 불확실성을 측정할 수 있어야 하고, 이를 통해 예측치의 신뢰구간도 구할 수 있고 모형의 과대적합도 방지할 수 있어야 합니다. 그래서 Exponential smoothing을 발전시킨 모형이 ETS 모형으로, Error, Trend, Seasonality 의 약자이고 exponential smoothing에 오차하잉 추가된 형태로 정의되며, 이 오차항은 평균이 0인 i.i.d한 정규분포를 가지고 있습니다.

ETS 모형은 시간에 따라 변하는 패턴을 예측하기 위해 오차(Error), 추세(Trend), 계절성(Seasonality)의 세 가지 구성요소를 조합하여 사용하는 시계열 모델입니다. 각각의 구성요소는 없음(None, N), 가법(Additive, A), 승법(Multiplicative, M) 중 하나로 선택할 수 있으며, 모델 이름은 세 요소를 조합하여 예를 들어 "AAN", "MAM", "ZAZ" 등으로 나타냅니다.

Darts의 AutoETS 모델에서는 model="ZZZ" 설정을 통해 세 가지 구성 요소를 모두 자동으로 최적화합니다.

모델 구성 예시

ETS 모델 구성 원리 (가법 오차 E(A,A,A) 예시)

ETS(A,A,A) 모형은 가법형 오차(Error), 추세(Trend), 계절성(Seasonality)을 가진 모델입니다. Exponential smoothing에서 추세와 계절성을 고려한 이전에 다룬 Holt-Winter 모형에서 오차 구조까지 명시적으로 포함한 확장형 모델이라고 보시면 됩니다. 먼저 아래의 예측식을 기반으로 합니다:

$$ y_t = l_{t-1} + b_{t-1} + s_{t-m} + \epsilon_t $$

여기서 \(\epsilon_t\)는 오차 항입니다. 이 오차를 바탕으로 세 가지 상태(state)를 업데이트합니다.

$$ \begin{aligned} l_t &= \alpha (y_t - s_{t-m}) + (1 - \alpha)(l_{t-1} + b_{t-1}) \\\\ b_t &= \beta (l_t - l_{t-1}) + (1 - \beta) b_{t-1} \\\\ s_t &= \gamma (y_t - l_{t-1} - b_{t-1}) + (1 - \gamma) s_{t-m} \end{aligned} $$

위 수식을 전개하여 오차항 \(\epsilon_t\) 기반의 형태로 바꿔보면 다음과 같이 유도됩니다:

$$ \begin{aligned} l_t &= l_{t-1} + b_{t-1} + \alpha \epsilon_t \\ b_t &= b_{t-1} + \beta \epsilon_t \\ s_t &= s_{t-m} + \gamma \epsilon_t \end{aligned} $$

이때 \(\alpha, \beta, \gamma\)는 각각 level, trend, seasonality의 민감도를 조절하는 계수입니다. 오차 \(\epsilon_t\)가 크면 세 요소가 크게 반응하고, 작으면 반응을 최소화합니다.

---

왜 State Space 모델인가?

ETS는 시간에 따라 상태가 변하는 구조를 가지므로 state-space model로 분류됩니다. 위의 수식에서 \(y_t\)는 측정식(measurement equation)이고, \(l_t, b_t, s_t\)를 갱신하는 수식은 상태식(state equations)이라 부릅니다.

---

E(M,A,A) 수식 유도 (승법 오차)

이번에는 오차항이 승법(multiplicative)인 경우를 살펴보겠습니다. 예측식은 다음과 같이 표현됩니다:

$$ y_t = (l_{t-1} + b_{t-1} + s_{t-m})(1 + \epsilon_t) $$

즉, 예측값 \(\hat{y}_t = l_{t-1} + b_{t-1} + s_{t-m}\)에 오차가 곱해지는 구조입니다. 이때 오차항 \(\epsilon_t\)는 다음과 같이 정의됩니다:

$$ \epsilon_t = \frac{y_t - \hat{y}_t}{\hat{y}_t} $$

상태 업데이트 수식도 \(\hat{y}_t\)에 비례하여 반응하게 됩니다:

$$ \begin{aligned} l_t &= l_{t-1} + b_{t-1} + \alpha \hat{y}_t \epsilon_t \\ b_t &= b_{t-1} + \beta \hat{y}_t \epsilon_t \\ s_t &= s_{t-m} + \gamma \hat{y}_t \epsilon_t \end{aligned} $$

---

기타 구조 예시

---

승법 Seasonality가 있는 경우

시작하기에 앞서 승법 Holt-Winter 모형을 다시 복습해봅시다:

\[ \begin{aligned} y_t &= (l_{t-1} + h b_{t-1}) s_{t-m} \\ l_t &= \alpha \frac{y_t}{s_{t-m}} + (1 - \alpha)(l_{t-1} + b_{t-1}) \\ b_t &= \beta (l_t - l_{t-1}) + (1 - \beta) b_{t-1} \\ s_t &= \gamma \frac{y_t}{l_{t-1} + b_{t-1}} + (1 - \gamma) s_{t-m} \end{aligned} \]

그렇다면 measurement equation은 \( y_t\) 에 오차항을 추가하면 됩니다.

$$ y_t = (l_{t-1} + h b_{t-1}) \cdot s_{t-m} + \epsilon_t $$

이 수식을 대입하여 이 경우 상태 업데이트는 다음과 같은 구조를 가집니다:

$$ \begin{aligned} l_t &= l_{t-1} + b_{t-1} + \alpha \frac{\epsilon_t}{s_{t-m}} \\ b_t &= b_{t-1} + \beta^* \frac{\epsilon_t}{s_{t-m}} \\ s_t &= s_{t-m} + \gamma \frac{\epsilon_t}{l_{t-1} + b_{t-1}} \end{aligned} $$

여기서 \( \beta^* = \alpha\beta \)입니다. 이제 유사한 방법으로 오차항이 승법인 E(M,A,M)을 고려해봅시다. 즉, \( \epsilon_t = \frac{y_t - (l_{t-1} + b_{t-1})s_{t-m}}{(l_{t-1} + b_{t-1})s_{t-m}}\) 이므로 measurement equation은 \( y_t = (l_{t-1} + b_{t-1})s_{t-m}(1+\epsilon_t) \)입니다. 이제 state equation 들에 대입해서 업데이트 식을 도출해봅시다.

$$ \begin{aligned} l_t &= l_{t-1} + b_{t-1} + \alpha (l_{t-1} + b_{t-1}) \epsilon_t \\ b_t &= b_{t-1} + \beta^* (l_{t-1} + b_{t-1}) \epsilon_t \\ s_t &= s_{t-m} + \gamma s_{t-m} \epsilon_t \end{aligned} $$

이제 이걸 기반으로 ETS(M,N,M) 모형은 ETS(M,A,M)에서 모든 t에 대해 \(b_t = 0 \)으로 놓으면 되고, E(A, N, M) 모형은 E(A, A, M) 에서 모든 t에 대해 \( b_t=0 \)으로 놓으면 됩니다. 승법 오차항 모형은 모든 시계열 값이 양의 값을 가지고 있을 때 유용하지만, 0또는 음의 값을 가지고 있으면 ETS 모형은 매우 불안정하므로 이 경우에는 사용하지 않는게 좋습니다. 모델이 수렴하지 않거나 예측이 불안정해질 수 있습니다. 이유는 매출, 애플의 주가, 비트코인 가격처럼 해당 시계열 데이터는 음수가 나올 수 없는 값인데, 예측값이 음수로 나와버리는 모형이 붕괴되는 상황이 발생 가능해서 그렇습니다. 이럴때는 additive를 쓰는게 맞겠죠.

---

ETS 상태공간(State Space) 모형 구조

ETS 모형은 아래 두 가지 방정식으로 구성된 상태공간 모델입니다.

$$ \begin{aligned} \text{(1) 측정방정식:} \quad & y_t = w(V_{t-1}) + r(V_{t-1}) \cdot \epsilon_t \\ \text{(2) 상태전이방정식:} \quad & V_t = f(V_{t-1}) + g(V_{t-1}) \cdot \epsilon_t \end{aligned} $$

여기서 \( V_t = [l_t, b_t, s_t]^T \)는 각각 level, trend, seasonality로 구성된 상태 변수 벡터입니다.

이 구조 덕분에 ETS는 level, trend, seasonality가 시간에 따라 어떻게 변하는지를 명확하게 반영할 수 있습니다.

AIC (Akaike Information Criterion) 기반 모델 선택

ETS 모형의 조합이 다양하기 때문에, Darts의 AutoETS(model="ZZZ")는 AIC를 활용하여 최적 모델을 자동으로 선택합니다.

$$ \text{AIC} = -2 \log(L) + 2k $$

AIC는 적합도와 모델 복잡도의 균형을 맞추기 위한 척도입니다.
⇒ AIC 값이 낮을수록 더 우수한 모델로 간주합니다.

따라서 AutoETS는 가능한 조합들 중 AIC가 가장 낮은 조합 (예: AAN, MAM, ZZZ 등)을 선택하여 예측을 수행합니다.

번외: Log-Likelihood란?

로그 가능도(log-likelihood)는 주어진 데이터가 특정 모델 하에서 발생할 확률의 로그입니다. 즉, 모델이 데이터를 얼마나 잘 설명하는지를 나타내는 지표입니다.

일반적으로 가능도 \( L \)는 너무 작은 값이 되기 때문에 로그를 취해서 계산합니다:

$$ \log(L) = \sum_{t=1}^{n} \log(P(y_t | \text{model})) $$

이 값이 클수록 (0에 가까울수록) 모델이 데이터를 잘 설명하는 것입니다.

번외: AIC와 BIC의 차이점

$$ \text{AIC} = -2 \log(L) + 2k \qquad \text{BIC} = -2 \log(L) + k \log(n) $$

두 지표 모두 값이 작을수록 더 좋은 모델로 간주되지만, 일반적으로:

Darts의 AutoETS는 기본적으로 AIC를 사용하여 모델을 선택합니다. 하지만 백엔드 라이브러리에 따라 BIC도 함께 계산 가능하며, 사용자가 직접 선택하여 사용할 수도 있습니다.

---

Darts로 AutoETS 적용 예시

실습은 Darts의 AutoETS로 ETS를 실행합니다. Darts의 ETS에서는 공변량 (covariates)을 추가해서 예측성능을 올릴 수 있습니다. Darts의 utility인 datetime_attribute_timeseries를 이용해서 cyclic=True를 지정하면 월효과를 Fourier 변환 i.e. \( \sin(\frac{2\pi t}{12}) + \cos(\frac{2\pi t}{12})\) 를 적용하게 됩니다. 미래 10개월을 예측하기 위해 add_length = 10을 지정해서 데이터 series 보다 10개월 더 연장하여 Fourier 변환하도록 하고 있습니다. 이렇게 정의된 future covariates는 model.fit을 할때 지정할 수 있습니다. AutoETS 옵션을 보면 예시에 사용되는 AirPassengers 데이터가 월별 시계열자료이므로 season_length=12를 주고 있습니다. 즉, season_length 는 seasonality의 주기를 지정합니다. model 3개의 문자로 ETS 모형을 지정합니다. Model의 문자는 N, A, M, Z중에 하나를 선택합니다. N은 None을, A는 additive를, M은 multiplicative를 그리고 Z는 \( AIC_c \)를 최소로 모형을 자동으로 선택하는 옵션입니다.

model = "ABC"로 표현되며 A는 ETS 모형의 error로 A, M, Z중에 하나를, B는 ETS 모형의 trend로 N, A, Z 중에 하나를, 그리고 C는 ETS 모형의 seasonality로 N, A, M, Z 중 하나를 선택할 수 있다. 예를 들어 model="ZAZ"는 error는 \( AIC_C \)를 기준으로 자동으로 A또는 M을 선택하고 trend는 A를, sesaonality는 \( AIC_C \) 를 기준으로 자동으로 N, A 또는 M을 선택합니다. dampled = False 또는 True를 선택해서 damped 모형 여부를 지정합니다. 

    from darts.datasets import AirPassengersDataset
    from darts.utils.timeseries_generation import datetime_attribute_timeseries
    from darts.models import AutoETS
    import pandas as pd

    series = AirPassengersDataset().load()
    train, val = series.split_before(pd.Timestamp("19580101"))
    future_cov = datetime_attribute_timeseries(series, "month", cyclic=True, add_length=10)

    model = AutoETS(season_length=12, model="ZAZ")
    model.fit(series, future_covariates=future_cov)
    pred = model.predict(10, future_covariates=future_cov)

    series.plot()
    pred.plot(label="ETS")
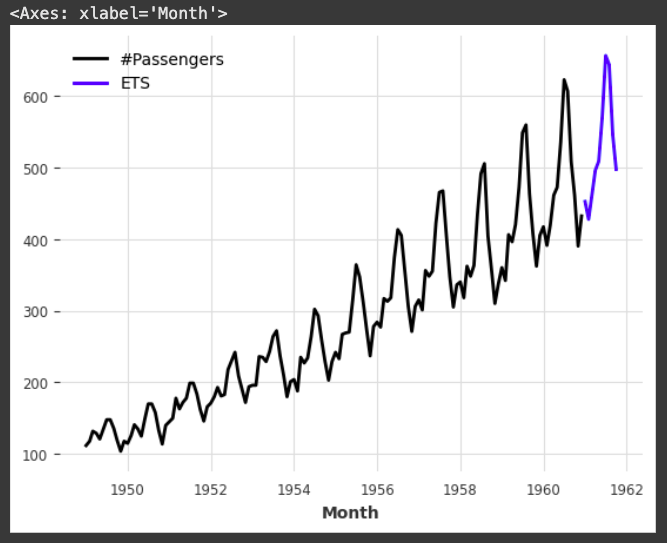
ETS 예측 결과 1

다음 예제로는 train 데이터를 이용해서 36개월로 구성된 검증데이터 + 6개월을 예측하기 위해 add_length = 6을 지정하고 있다. model="ZZZ"를 지정하여 ETS의 각 구성요소를 모두 자동으로 선택하도록 하고 있으며 predict()에 새롭게 num_samples=500을 지정하고 있습니다. 이렇게 되면 예측 경로 500개를 생성해서 monte carlo 확률적 예측 방법으로 예측치의 신뢰도를 측정할 수 있습니다. 예측치의 산포도가 좁을수록 신뢰고다 높다고 말합니다. 

    from darts.datasets import AirPassengersDataset
    from darts.utils.timeseries_generation import datetime_attribute_timeseries
    from darts.models import AutoETS
    import pandas as pd

    series = AirPassengersDataset().load()
    train, val = series.split_before(pd.Timestamp("19580101"))
    future_cov = datetime_attribute_timeseries(series, "month", cyclic=True, add_length=10)

    model_auto = AutoETS(season_length=12, model="ZZZ")
    model_auto.fit(train, future_covariates=future_cov)
    pred = model_auto.predict(42, future_covariates=future_cov, num_samples=500)
    pred.values()
    series.plot()
    pred.plot(label="ETS_auto")
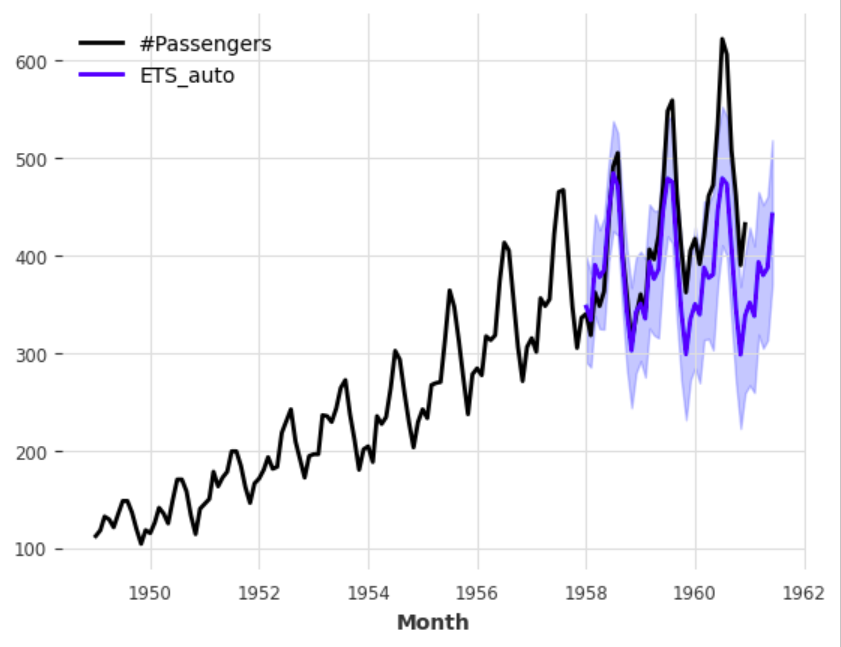
ETS 예측 결과 2

다음은 model = "ZAZ" 로 지정하여 확률적 예측 결과를 보여주고 있습니다. 예측칙의 굵은 파란선은 확률적 예측 500개의 median으로 model="ZZZ"보다는 우수한 예측치를 보여주고 있습니다. 

    from darts.datasets import AirPassengersDataset
    from darts.utils.timeseries_generation import datetime_attribute_timeseries
    from darts.models import AutoETS
    import pandas as pd

    series = AirPassengersDataset().load()
    train, val = series.split_before(pd.Timestamp("19580101"))
    future_cov = datetime_attribute_timeseries(series, "month", cyclic=True, add_length=10)

    model_auto = AutoETS(season_length=12, model="ZAZ")
    model_auto.fit(train)
    pred = model_auto.predict(42, num_samples=500)
    pred.values()
    series.plot()
    pred.plot(label="ETS_auto")
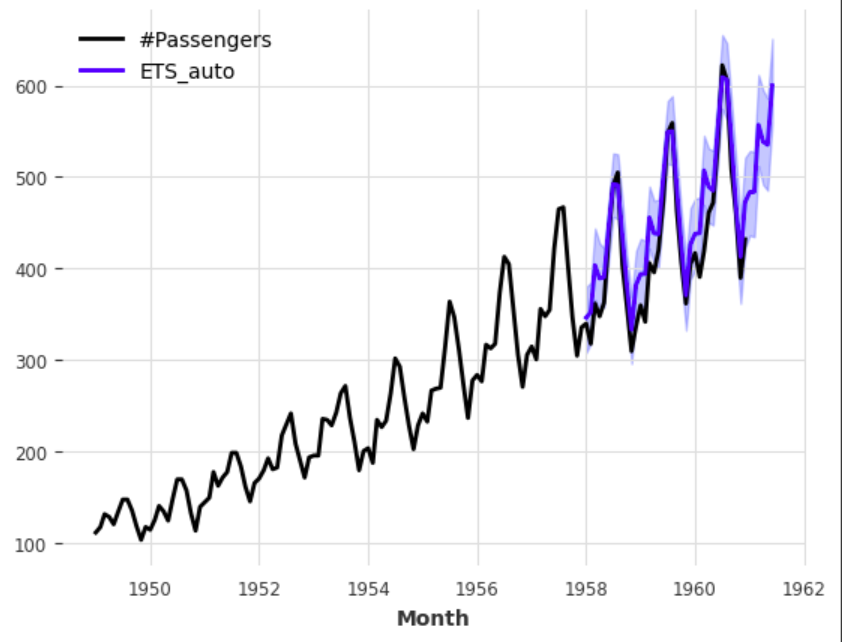
ETS 예측 결과 3

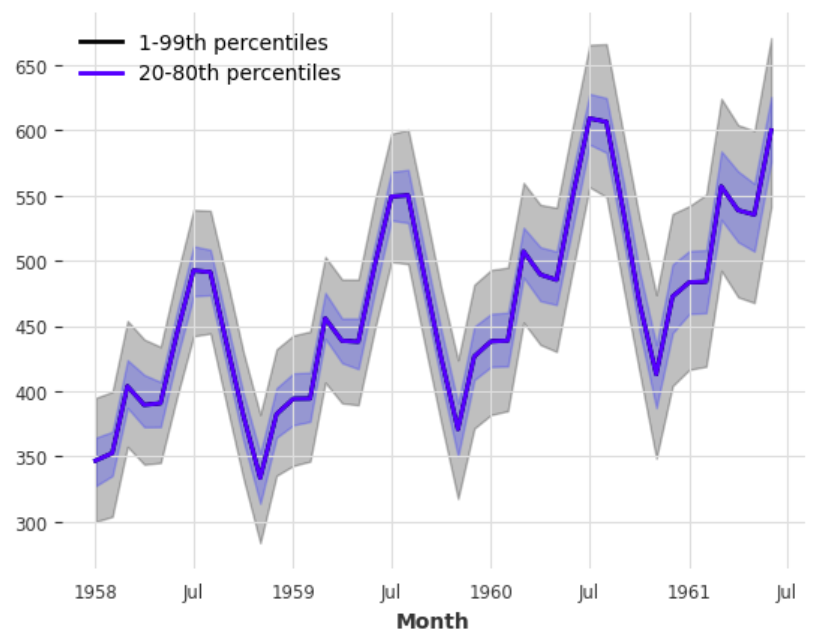
아래처럼 500개의 확률적 예측치로부터 quantile을 구해서 monte carlo 신뢰구간도 구할 수 있습니다.

ETS 예측 결과 4

AutoETS를 비트코인 예측에 적용

이제 AutoETS를 이용해서 비트코인 1시간봉 종가 예측에 적용하는 예제를 보여드리겠습니다. CCXT로 MEXC에서 비트코인 1시간봉 데이터 500개를 들고와서 예측을 수행합니다. 

    import ccxt
    import pandas as pd
    import matplotlib.pyplot as plt
    from darts import TimeSeries
    from darts.models import AutoETS


    # 1. 비트코인 1시간봉 데이터 로드
    exchange = ccxt.mexc()
    symbol = "BTC/USDT"
    timeframe = "1h"
    ohlcv = exchange.fetch_ohlcv(symbol, timeframe, limit=500)
    df = pd.DataFrame(ohlcv, columns=["timestamp", "open", "high", "low", "close", "volume"])
    df["datetime"] = pd.to_datetime(df["timestamp"], unit="ms")
    df.set_index("datetime", inplace=True)

    # 2. Darts TimeSeries로 변환 (종가 사용)
    series = TimeSeries.from_dataframe(df, value_cols="close")

    # 3. train/val 분리 (최근 48시간 예측을 위해 분리)
    train, val = series[:-48], series[-48:]

    # 4. ETS 모델 초기화 및 학습
    model = AutoETS(season_length=24, model="ZZZ")  # 24시간 = 1일 주기
    model.fit(train)

    # 5. 예측 (48시간, Monte Carlo 500개 경로 기반)
    forecast = model.predict(n=48, num_samples=500)

    # 6. 시각화
    series.plot(label="Actual BTC/USDT")
    forecast.plot(label="ETS Forecast")
    forecast.plot(low_quantile=0.1, high_quantile=0.9, label="80% CI")

    plt.title("BTC/USDT 1H Forecast with AutoETS")
    plt.legend()
    plt.show()
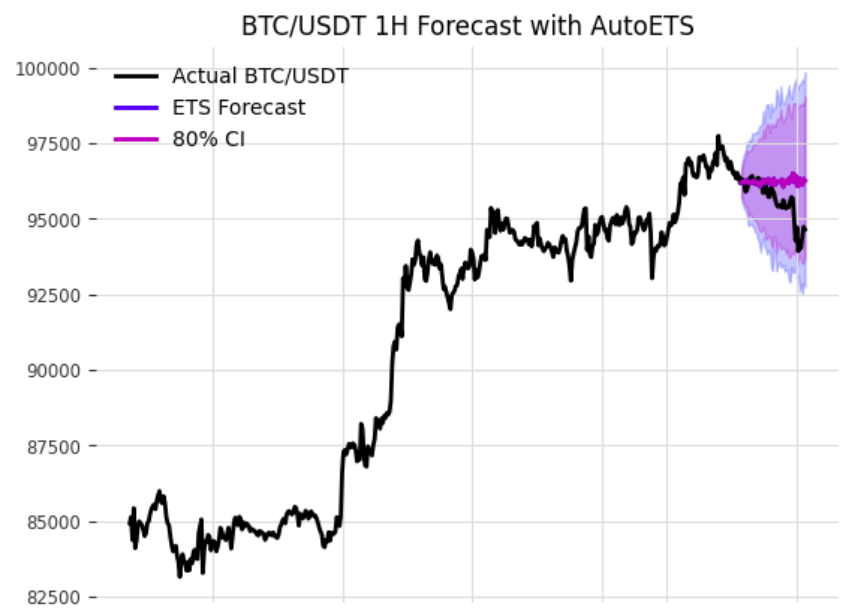
ETS 예측 결과 5

예상한것처럼, AutoETS는 내부적으로 지수 평활 기반 모델이고 노이즈가 많고 비선형적인 데이터에 대한 예측 능력은 떨어져 보입니다. 그리고 "ZZZ"는 내부적으로 트렌드 구성 (A / N / A_d) 을 선택적으로 반영하지만 데이터가 충분하지 않거나 노이즈가 많으면 추세 없는 구성을 선택할 수 있고, 결과적으로 평균 수준을 예측하는 모델로 수렴한것을 볼 수 있습니다. 재밌는점은 ETS모델이 정밀한 단일값을 맞추지느 못했지만 예측 경로 분포로 만들어진 신뢰구간 (80% confidence interval) 안에 실체가 포함되었기 때문에 해당 예측은 확률적으로 신뢰할 수 있는 수준이라고 생각할수는 있습니다.