Simple Quant Labs
Holt-Winters Seasonal Model
Holt-Winters 모형은 지수 평활법에서 발전한 형태로, 레벨(level), 추세(trend), 계절성(seasonality)을 모두 고려한 예측 방법입니다. 이전 Holt's Linear Trend 모델에서 추세만 고려했다면, 이제는 추세와 계절성 둘 다 고려하는거죠.
기본적으로 가법(additive) 모델과 승법(multiplicative) 모델 두 가지가 있으며, 데이터의 계절성 패턴이 level의 크기와 독립적이면 가법, 비례적으로 변하면 승법을 사용합니다.
가법 모델 (Additive)
계절성이 일정한 절대 크기로 반복되는 경우 사용합니다.
$$ \begin{align*} l_t &= \alpha (y_t - s_{t-m}) + (1 - \alpha)(l_{t-1} + b_{t-1}) \\ b_t &= \beta (l_t - l_{t-1}) + (1 - \beta) b_{t-1} \\ s_t &= \gamma (y_t - l_{t-1} - b_{t-1}) + (1 - \gamma) s_{t-m} \\ \hat{y}_{t+h|t} &= l_t + h b_t + s_{t+h-m(k+1)} \end{align*} $$
승법 모델 (Multiplicative)
계절성이 level에 비례하여 커졌다 작아지는 경우 사용합니다.
$$ \begin{align*} l_t &= \alpha \left(\frac{y_t}{s_{t-m}}\right) + (1 - \alpha)(l_{t-1} + b_{t-1}) \\ b_t &= \beta (l_t - l_{t-1}) + (1 - \beta) b_{t-1} \\ s_t &= \gamma \left(\frac{y_t}{l_{t-1} + b_{t-1}}\right) + (1 - \gamma) s_{t-m} \\ \hat{y}_{t+h|t} &= (l_t + h b_t) \cdot s_{t+h-m(k+1)} \end{align*} $$
여기서 \( m \)은 계절 주기 (예: 월별 데이터일 경우 12),
\( k = \left\lfloor \frac{h-1}{m} \right\rfloor \) 은 계절 인덱스를 반복 맞추기 위한 정수입니다.
\( \alpha, \beta, \gamma \)는 각각 레벨, 추세, 계절성에 대한 반응도입니다.
업데이트 식에 대한 쉬운 설명
$$ \begin{align*} l_t &= \alpha (y_t - s_{t-m}) + (1 - \alpha)(l_{t-1} + b_{t-1}) \\ \end{align*} $$ level 업데이트는 현재 관측값 \( y_t \)에서 계절성을 제거한 값을 통해 순수한 level 을 파악하고, 예측한 level \( l_{t-1} + b_{t-1} \) 과 적절히 가중 평균한 것입니다. $$ \begin{align*} b_t &= \beta (l_t - l_{t-1}) + (1 - \beta) b_{t-1} \\ \end{align*} $$ trend 업데이트는 level의 변화량 \(l_t - l_{t-1}\)과 이전 추세와의 가중 평균으로 업데이트 한다고 보면 됩니다. $$ \begin{align*} s_t = \gamma (y_t - l_{t-1} - b_{t-1}) + (1 - \gamma) s_{t-m} \end{align*} $$ 마지막으로 계절성 업데이트로는 \( y_t - l_{t-1} - b_{t-1} \), 즉 실제 관측값에서 비계절적인 부분을 제거한 항과 \( s_{t-m} \), 과거 동일한 계절 시점의 계절성과의 가중평균을 기반으로 업데이트 한다.
가법 vs 승법 선택 기준
그럼 “level과 무관하게 주기성이 있다”는 건 무슨 뜻일까요?
▶ 예시 1: 가법 모델이 적절한 경우
매출이 계절에 따라 항상 +20 / -20씩 변한다고 해볼게요.
- 여름에는 항상 +20
- 겨울에는 항상 -20
그런데 전체 매출 규모가 100 → 110 → 120처럼 오르고 있다면?
→ 계절 효과는 level과 관계없이 항상 일정하므로 ➤ 가법 모델이 적절합니다.
반대로 “level에 따라 계절성이 달라진다”는 건?
▶ 예시 2: 승법 모델이 적절한 경우
- 초반에 매출이 100인데 여름에 20% 상승 → 120
- 나중에 매출이 300이 되면 여름엔 20% 상승 → 360
즉, 계절 효과가 비율로 작용하고 있고, 매출이 클수록 계절 효과도 커집니다.
→ 이런 경우 ➤ 승법 모델이 적절합니다.
요약
Holt-Winters 모델은 추세와 계절성을 모두 반영하여 더 현실적인 시계열 예측이 가능합니다. 계절성이 명확한 데이터에 특히 유리하며, level 수준에 따른 계절 영향의 형태에 따라 가법 또는 승법 모델을 선택합니다.
Darts 활용 예제
Darts 라이브러리의 ExponentialSmoothing을 사용하면 trend와 seasonality 모드 및 damped 옵션을 간단히 설정할 수 있습니다.
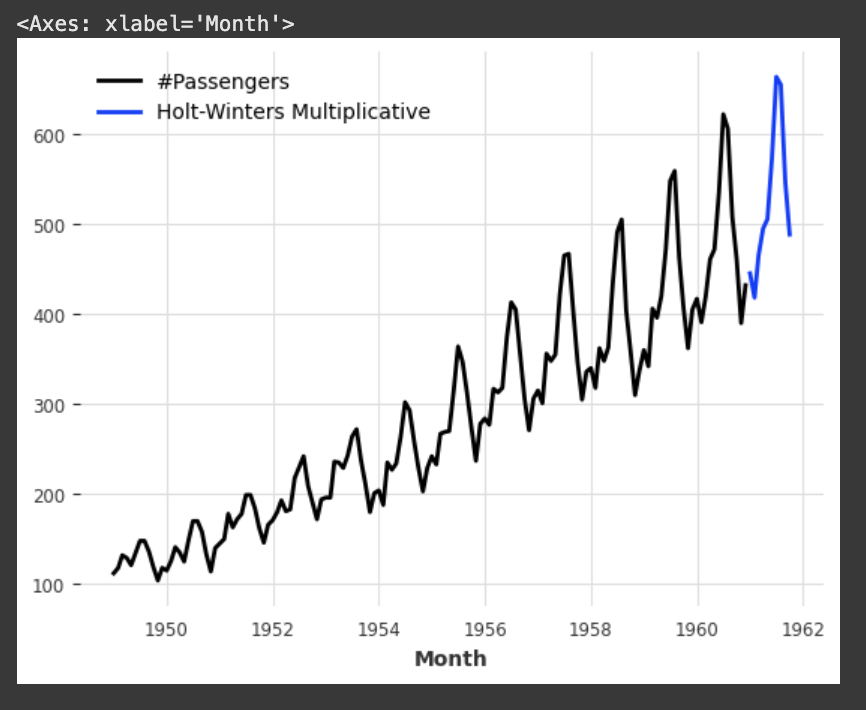
아래는 승법 Holt-Winters 모형을 적용하여 AirPassengers 데이터를 기반으로 미래 10개월을 예측한 예시입니다.
from darts.datasets import AirPassengersDataset
from darts.models import ExponentialSmoothing
from darts.utils.utils import ModelMode, SeasonalityMode
series = AirPassengersDataset().load()
model = ExponentialSmoothing(
trend=ModelMode.ADDITIVE,
damped=False,
seasonal=SeasonalityMode.MULTIPLICATIVE
)
model.fit(series)
pred = model.predict(10)
series.plot()
pred.plot(label="Holt-Winters Multiplicative")
위 예시에서 trend는 ModelMode.ADDITIVE (기본값), damped는 False (기본값), seasonal은 SeasonalityMode.MULTIPLICATIVE로 지정하여, 승법 계절성을 반영한 모델을 설정합니다.
추세 없이 계절성만 반영한 exponential smoothing도 가능하며, 이는 종종 단순 계절 모델(seasonal exponential smoothing)로 분류되기도 합니다. 다만, 실무에서는 trend와 seasonality를 함께 반영한 Holt-Winters 모델이 더 일반적으로 사용됩니다.