Simple Quant Labs

Random Walk

Naive forecast는 \( y_t \)는 비정상 (non-stationary) 시계열이지만, \( y_t - y_{t-1} \) 이 정상 시계열일 때 사용하는 모형입니다. 이 차분(differencing)은 시계열이 1차 추세(trend)를 가질 때 비정상성을 제거하는 데 유용합니다.

즉,

$$ y_t = y_{t-1} + \varepsilon_t $$

위 모형에서 \( y_t - y_{t-1} \)는 평균이 0인 white noise를 따른다고 가정하며, 이러한 과정을 random walk라고 합니다. 따라서 조건부 기댓값은 다음과 같습니다:

$$ E(y_t \mid y_{t-1}) = y_{t-1} $$

이는 \( y_t \)의 가장 좋은 예측치는 바로 이전 시점 값 \( y_{t-1} \)이라는 뜻입니다. 미래 h 시점 예측은 다음과 같으며, 이를 naive forecast라고 부릅니다:

$$ \hat y_{T+h \mid T} = y_T \quad \text{for } h = 1, 2, ..., l $$

---

계절성 시계열의 naive 예측 (Seasonal Naive Forecast)

시계열 데이터가 seasonality를 가지는 경우, 예측값은 과거 동일 주기의 값을 참고하여 계산할 수 있습니다. 예를 들어 주간 seasonality를 가진 일일 데이터라면, 오늘의 값은 7일 전의 값에 영향을 받습니다.

seasonality의 주기 \( m \)에 대해 다음처럼 정의할 수 있습니다:

• Weekly seasonality → \( m = 7 \)
• Monthly seasonality → \( m = 30.4 \)
• Yearly seasonality → \( m = 365.25 \)

$$ y_t = y_{t-m} + \varepsilon_t $$

\( y_t - y_{t-m} \)가 평균 0인 white noise라면, 가장 좋은 예측값은 \( y_{t-m} \)입니다. 이러한 모형을 seasonal random walk라고 합니다.

---

Drift를 가진 Random Walk

만약 \( y_t - y_{t-1} \)의 평균이 0이 아니라면 다음과 같이 표현됩니다:

$$ y_t - y_{t-1} = \theta + \varepsilon_t \quad \Rightarrow \quad y_t = y_{t-1} + \theta + \varepsilon_t $$

이때 \( y_t \)는 뚜렷한 선형 추세를 가지며, 이를 random walk with drift라고 합니다.

---

💻 Darts로 구현하는 예측

다음은 Darts 라이브러리를 활용한 실습 예제입니다:

    from darts.datasets import AirPassengersDataset
    import pandas as pd
    from darts.models import NaiveSeasonal

    series = AirPassengersDataset().load()
    series.plot()
    train, val = series.split_before(pd.Timestamp("19580101"))

    naive_model = NaiveSeasonal(K=1)
    naive_model.fit(train)
    naive_forecast = naive_model.predict(36)
    series.plot(label="actual")
    naive_forecast.plot(label="naive forecast (K=1)")
    

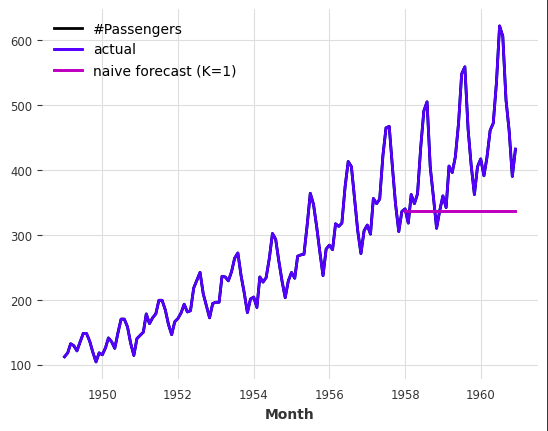
→ 학습 데이터의 마지막 값을 반복하여 예측하므로 단순하지만 baseline으로 적합합니다.

✅ Seasonal Naive 예측 (K=12)

    seasonal_model = NaiveSeasonal(K=12)
    seasonal_model.fit(train)
    seasonal_forecast = seasonal_model.predict(36)
    series.plot(label="actual")
    seasonal_forecast.plot(label="naive forecast (K=12)")
    

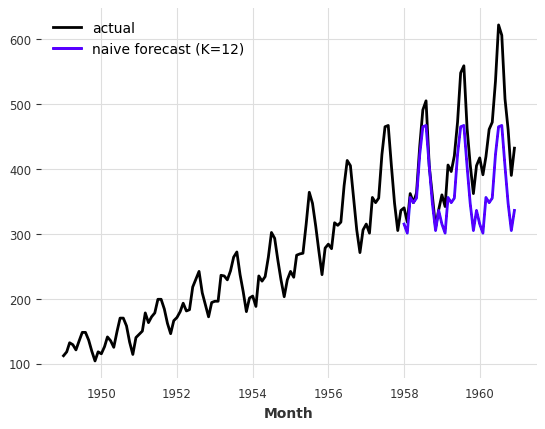
→ 학습 데이터 마지막 12개를 3번 반복하여 예측. 성능 개선됨.

📈 Drift 포함한 Random Walk

    from darts.models import NaiveDrift
    drift_model = NaiveDrift()
    drift_model.fit(train)
    drift_forecast = drift_model.predict(36)
    combined_forecast = drift_forecast + seasonal_forecast - train.last_value()
    series.plot()
    combined_forecast.plot(label="combined")
    drift_forecast.plot(label="drift")
    

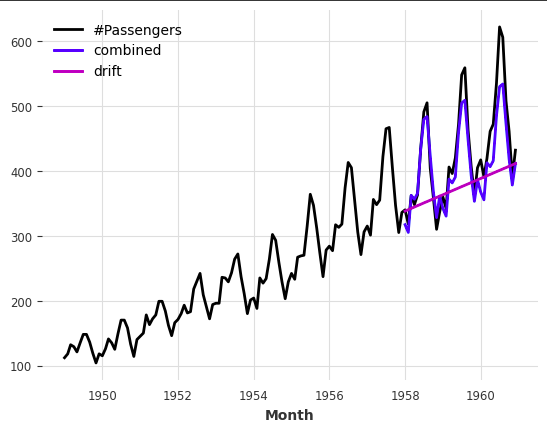
→ 단순 선형회귀처럼 동작하며, drift + seasonality 조합이 더 좋은 결과를 냅니다.